Medidas invariantes y Teorema de Descomposición Ergódica.

In Análisis Real y Complejo, Probabilidad y Estadística, Sistemas Dinámicos on jueves 29, abril, 2010 at 10:41 am

por Rafael Potrie

Consideremos un homeomorfismo $f:X\to X$ donde $X$ es un espacio métrico compacto. Decimos que una medida de probabilidad $\mu$ en $X$ es $f$ -invariante, si se cumple que $\mu(f^{-1}(A))=\mu(A)$ para todo conjunto medible $A$ .

Estas medidas son generalmente muy útiles para estudiar la dinámica del homeomorfismo como se ver rápidamente al ver los enunciados del Teorema de Recurrencia de Poincare o el Teorema Ergódico de Birkhoff (una prueba de este último bastante simple se encuentra en este link de este mismo blog).

Hay cierto tipo de medidas invariantes que son preferidas, por ser de alguna manera, indescomponibles, estas son llamadas medidas ergódicas y verifican que si $A$ es un conjunto $f-$ invariante, entonces, su medida es cero o uno.

Mediante resultados clasicos de analisis funcional, se puede probar que en general, existen medidas invariantes (para un homeomorfismo de un espacio métrico compacto) e incluso medidas ergódicas. Lo primero, es una consecuencia relativamente directa del Teorema de Banach-Alaoglu, que garantiza que el espacio de medidas de probabilidad es compacto con la topología débil (y por tanto, si se construye una medida «cada vez más invariante», su límite será invariante) y lo segundo surge del Teorema de Krein-Milman ya que dado que las medidas invariantes forman un convexo compacto, tienen que tener elementos extremales (que serán las medidas ergódicas). Sin embargo, este último teorema, que nos permite aproximar toda medida invariante por combinaciones convexas de medidas ergódicas, no termina de mostrar realmente como es esta descomposición.

El objetivo de esta nota, es presentar un formalismo, el de las particiones medibles y medidas condicionales que permiten dar un sentido a dicha descomposición.

Desintegración de medidas y particiones medibles.

Consideremos un espacio métrico compacto $X$ y $\mu$ una probabilidad de borel. Si $\mathcal P$ es una partición de $X$ en conjuntos medibles, tenemos definida naturalmente una proyección $\pi: X \to \mathcal P$ que manda cada punto en el átomo de la partición que lo contiene ( $\pi(x) = P \in \mathcal P$ tal que $x\in P$ ).

De esta manera, podemos considerar naturalmente una sigma álgebra en $\mathcal P$ conveniendo que un subconjunto $\mathcal Q \subset \mathcal P$ es medible si $\pi^{-1} (\mathcal Q)$ es medible y podemos pasar la medida $\mu$ a una medida $\hat \mu$ en $\mathcal P$ como $\hat \mu (\mathcal Q) = \mu (\pi^{-1}(\mathcal Q)$ .

Lo que voy a decir ahora está muy relacionado con la Esperanza Condicional aunque estaría bueno comprender un poco más en profundidad dicha relación.

Supongamos primero que la partición $\mathcal P$ es finita (lo que voy a decir vale para numerable, pero más fácil asi), entonces, podemos considerar en cada átomo $P \in \mathcal P$ , una medida de probabilidad $\mu_P$ de forma tal que dado un conjunto medible $E \subset X$ , tenemos que

$\mu(E) = \sum_{P \in \mathcal P} \mu_P(E) \hat \mu(\{P\}) = \int (\int 1_E d\mu_P) d\hat \mu$

donde $1_E$ es la función caracteristica de $E$ . La última igualdad no es más que una cuestión notacional que permite imaginarse la generalización a particiones más generales.

Decimos entonces que la medida $\mu$ admite una desintegración en medidas condicionales con respecto a la partición $\mathcal P$ si existe una familia $\{\mu_P \ : \ P\in \mathcal P\}$ de medidas de probabilidad tales que $\mu_P(P)=1$ para $\hat \mu$ -casi todo $P \in \mathcal P$ y se cumple que para toda función continua $\varphi: X \to \mathbb{R}$ se tiene que la función $P \mapsto \int \varphi d\mu_P$ es medible y:

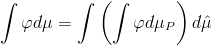No es dificil ver que si una medida $\mu$ admite una desintegración en medidas condicionales, esta es escencialmente única, es decir, si consideramos dos diferentes, coinciden en un conjunto de $\hat \mu$ medida total.

Vamos a enunciar un Teorema debido a Rokhlin que da una condición bastante laxa en la partición que garantiza la existencia de dicha deisntegración.

Definición Una partición $\mathcal P$ de $X$ en conjuntos medibles es una partición medible si existen particiónes numerables $\mathcal P_1 ,\ldots, \mathcal P_n, \ldots$ cada una mas fina que la siguiente tal que $\mathcal P = \bigvee_{n\geq 1} \mathcal P_n$ .

Notar que esta definición es bastante general, en particular, contiene a las particiones numerables, a la partición en los puntos, y a por ejemplo si consideramos un espacio producto $X \times Y$ con $X$ e $Y$ compactos se cumple que la partición en conjuntos de la forma $\{x\}\times Y$ es una partición medible.

Se cumple el siguiente Teorema cuya prueba se puede encontrar aqui (no es muy dificil, la construcción es relativamente la natural, hay cosas que probar igual)

Teorema (Rokhlin) Sea $\mathcal P$ una partición medible de $X$ . Entonces, existe una desintegración de $\mu$ en medidas condicionales.

Teorema de Descomposición Ergódica.

Lo que viene asume familiaridad con el Teorema de Birkhoff (ver aqui por ejemplo).

Sea $f:X\to X$ un homeomorfismo. El Teorema de Birkhoff garantiza la existencia de un conjunto $B_f$ que mide uno para cualquier medida invariante tal que se tiene que si $x\in B_f$ y $\varphi: X \to \mathbb{R}$ es una función continua, entonces, existe el límite

$\lim_{n\to \infty} \frac 1 n \sum_{i=0}^{n-1} \varphi\circ f^i(x) = \tilde \varphi(x)$

Le llamamos a $\tilde \varphi(x)$ el promedio de Birkhoff de la función $\varphi$ en el punto $x$ .

Podemos entonces definir una relación de equivalencia natural en $B_f$ dada por $x_1 \sim x_2$ siempre y cuando para toda función continua $\varphi:X\to \mathbb{R}$ se tiene que $\tilde \varphi(x_1)= \tilde \varphi(x_2)$ .

Esto define una partición $\mathcal P$ de $X$ dada por las clases de equivalencia de esta relación y agregando un átomo $X-B_f$ que medirá cero para cualquier medida invariante.

No es dificil probar que efectivamente $\mathcal P$ es una partición medible, de hecho, para que dos puntos sean equivalentes, alcanza que sus promedios de Birkhoff coincidan para un conjunto denso numerable de funciones continuas y claramente esto lo podemos expresar mediante numerables condiciones con lo cual confirmamos lo afirmado.

Consideramos entonces una medida invariante $\mu$ para $f$ . Entonces, el Teorema de Rokhlin nos permite desintegrarla en medidas $\mu_P$ para cada $P\in \mathcal P$ y que se cumpla que para casi todo $P$ con respecto a $\hat \mu$ , se tiene que $\mu_P(P)=1$ . Como en cada $P \in \mathcal P$ (salvo $X-B_f$ ) los promedios en funciones continuas coinciden, obtenemos rápidamente que la medida $\mu_P$ es ergódica para casi todo $P$ con respecto a $\hat \mu$ .

Obtenemos entonces el siguiente Teorema que se puede probar independientemente del Teorema de Rokhlin.

Dado un punto $x$ , definimos la medida $\mu_n(x)= \frac 1 n \sum_{i=0}^{n-1} \delta(f^i(x))$ .

Teorema (Descomposición Ergódica) Existe un conjunto de probabilidad total $\Sigma$ (mide uno respecto a toda medida $f$ -invariante) tal que si $x\in \Sigma$ , entonces el limite débil de las medidas $\mu_n(x)$ es una medida ergódica $\mu(x)$ . Además, si $\varphi \in L^1(\mu)$ entonces, es integrable para $\mu_x$ para $\mu$ -casi todo $x$ y se cumple que

$\int_X (\int_X \varphi d\mu_x) d\mu = \int_X \varphi d\mu$

Otros intereses de la desintegración de medidas respecto a una partición.

Para terminar, voy a comentar un poco otros contextos en los que surge el interés en desintegrar medidas respecto a una partición. Lamentablemente, no tengo espacio para introducir todos los conceptos que voy a utilizar.

La idea es la siguiente, cuando $f:M\to M$ es un difeomorfismo de Anosov, no es dificil ver que si hay algún punto periódico para el cual el determinante del diferencial es diferente de uno, entonces, no puede haber una medida absolutamente continua invariante por $f$ (la escencia de esto, es que la existencia de uno implica la existencia de un conjunto denso de puntos periódicos con esta propiedad, y si hay una densidad de una medida invariante tiene que anularse en cada uno de estos puntos).

Esto nos genera el siguiente problema: hay alguna medida invariante «preferida» para este difeomorfismo (obviamente, si preservara una absolutamente continua respecto a Lebesgue tendría que ser ella la »preferida»). La respuesta no es clara ya que la pregunta es ambigua (y de hecho, hay muchas posibles medidas «preferidas» dependiendo de que queramos de ellas, el sambita nos podria contar de eso, je). Sin embargo, hay una respuesta posible que es la existencia de medidas SRB (Sinai-Ruelle-Bowen) cuando el difeomorfism0 es de clase $C^2$ .

Se cumple el siguiente Teorema

Teorema Sea $f:M \to M$ un difeomorfismo de Anosov de clase $C^2$ transitivo. Entonces, existe una única medida invariante $\mu^+$ de Borel tal que es límite de $\mu_n(x)$ para Lebesgue casi todo punto $x\in M$ . Además, esta medida es absolutamente continua respecto a la foliación inestable, esto es, en todo punto, se puede considerar una caja foliada por variedades inestables y la desintegración de $\mu^+$ respecto a dicha partición (en hojas inestables) verifica que para casi toda hoja, la medida alli es absolutamente continua respecto a Lebesgue en la hoja.

La hipotesis de que sea $C^2$ es clave ya que da continuidad absoluta de las foliaciones cosa que falla en el caso $C^1$ (esto tiene que ver con que hay herraduras de medida de Lebesgue positiva para difeomorfismos $C^1$ y no para difeomorfismos de clase $C^2$ ). Todo esto es relativamente técnico y dificil de contar mejor en un post, pero vale la pena leer el Capítulo III.2 del libro de Mañe, aunque sea hasta que empiezan las pruebas.

▶ 10 respuestas

En el último teorema, la propiedad que la desintagración sea abs. cont. respecto Lebesgue no es lo que determina las SRB, no?. Me parece que se verifica para cualquier estado de equilibrio.

La idea de desintegrar una medida invariante en la foliación inestable está excelente, se usa mucho para estudiar geometría, por ejemplo el flujo geodésico: pasas de una medida invariante por el flujo a una medida (quasi)invariante por la foliación estable (=flujo de horocíclos) que es mucho mas rígido.

Responder

Andrés Sambarino 3 May 2010 at 8am
No se demasiado de esto, y no hay entrada en Wikipedia ni Scholarpedia (aun, esa está en camino, y va a escribirla, cuando no, Sinai) aun. Si no me equivoco, hay dos «tipos» de medidas interesantes desde este punto de vista:

Los $u$ -estados de Gibbs, que son las medidas cuya desintegración es absolutamente continua en variedades inestables y por otro lado, las medidas físicas que son las que la cuenca (es decir, el conjunto de puntos cuyos promedios convergen a esa medida) tiene medida positiva.

La definición «estandar» de SRB es que verifique ambas propiedades y lo que probaron Sinai-Ruelle y Bowen es que para diffeos Axioma A de clase $C^2$ tienen finitas medidas de ese tipo y que su cuenca cubre un conjunto de medida de Lebesgue total.

Hay otras medidas muy interesantes y que para mi estan un poco más relegadas y no deberian que son las medidas de entropía maximal cuyo nombre explica que son.

Responder

rpotrie 3 May 2010 at 1pm
Respecto a lo último (importancia de medidas de máxima entropía): tal cual, y como ejemplo están los polinomios (en la esfera): las únicas medidas físicas que podés poner ahí son deltas de dirac en atractores, superatractores o parabólicos, es decir, medidas que no aportan mucho. En ese caso (para cualquier función racional de hecho) tenés una medida (única además) de máxima entropía (log del grado d) y esa es la mas útil.

Aprovechando lo que comentaste de la convergencia débil *, una manera de construir esa medida es pegar un punto (no excepcional, o sea que tenga preimagenes) e ir promediando (dividiendo por d^n) las deltas de dirac en las preimagenes n-ésimas (fue Manhé quien construyó eso y quien provó la unicidad, vamo y vamo!!).

Responder

Pablo Guarino 4 May 2010 at 8pm
- Tremendo ejemplo! ahi no queda duda que esas medidas le pintan la cara a las SRB.
  
  Una pregunta sobre eso…. en el caso de Julia de medida positiva, sabes si la medida de máxima entropia tiene cuenca con medida positiva? porque ahi podría llegar a ser, al menos a priori (o mismo en el caso que el Julia sea todo, será que la medida de entropia maximal tiene algo que ver con Lebesgue?).
  
  Responder
  
  rpotrie 4 May 2010 at 8pm
  - Siempre (para cualquier función racional en la esfera) tenés que el soporte de la medida de máxima entropía es el Julia entero, lo cual muestra como las preórbitas de un punto genérico (no excepcional, todos salvo dos a lo sumo) se distribuyen uniformemente alrededor del Julia.
    
    O sea que en los casos que nombrás (Julias con medida positiva, Fatou vacío) sabemos que el soporte de la medida tiene media de Lebesgue positiva. Ahora bien, tu pergunta es mas delicada, porque los puntios del Julia que estén en la cuenca de la medida precisan tener órbitas transitivas y bien distribuidas. Esos tienen medida positiva? No sé.
    
    Al respecto del primer párrafo, aprovecho para decir que nada de eso se sabe en dimensión mayor (por ejemplo, difeos polinomiales en C^2). Hay medida de máxima entropía, su soporte está contenido en el Julia (claro), pero no se sabe si es todo el Julia (en el caso hiperbólico sí, pero en general está en abierto).
    
    Pablo Guarino 5 May 2010 at 3pm
  - Hay una buena pregunta ahi…. porque sería interesante saber si en el caso que tenga medida positiva el Julia (mismo siendo todo) hay un conjunto de medida positiva donde el promedio de las deltas tienda a la de máxima entropia.
    
    En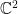 $\mathbb{C}^2$ te deseo suerte, je. De paso, para escribir en latex, hay que escribir como escribirias, pero en vez de rodear por $, lo que haces es poner $latex despues pones la formula y despues cerras con otro signo de pesos.
    
    rpotrie 5 May 2010 at 9pm
Otro comentario sobre las medidas SRB y de máxima entropía, pero para flujos:

Si tenes un atractor hiperbólico para un flujo podés reparametrizar el flujo para que las medidas SRB y de máxima entropía coincidan.

Un ejemplo es el caso del flujo geodésico en curvatura -1, ahí ya son la misma.

Esto es consecuencia de 2 cosas, el estado de Gibbs de un potencial $F$ y el de $F+constante$ es el mismo; y del teorema de Livsic: el estado de Gibbs de $F$ solo depende del promedio de $F$ en las órbitas periódicas.
El potencial que determina la SRB es «el valor propio inestable» y cuando calculás explícitamente el promedio en las órbitas periódicas (poniendo Lebesgue de masa 1 en la órbita periódica) te da constante, o sea que es el estado de Gibbs de la función 0, que es la medida de máxima entropía.

Responder

Andrés Sambarino 12 May 2010 at 6am
- Lo que queres decir es que reparametrizando podes «ajustar» los valores propios en las ‘orbitas peri’odicas o entendi cualquiera?
  
  Responder
  
  rpotrie 12 May 2010 at 7am
Ahí va. La idea es esa, ajustas los valores propios en las orbitas periódicas para aplicar el teorema de Livsic y obtener, con un argumento como el del flujo geodésico, que la SRB del nuevo flujo es la de máxima entropía.

Igual atenti que cuando reparametrizás hay que «ajustar» las medidas invariantes para que sigan siendo invariantes.

Todo esto está en el asterisque de Parry-Polliott.

Responder

Andrés Sambarino 12 May 2010 at 8am
La verdad que está tremenda la pregunta, porque en definitiva en hiperbolicidad lo que pasa es que para difeos son importantes las dos, para dinámica holomorfa la SRB no sirve pa’ nada (si entendí lo que dice el guarino), y para flujos son «la misma».

Responder

Andrés Sambarino 12 May 2010 at 8am