por Rafael Potrie
Uno de los problemas más difíciles de la topología algebraica es determinar los con
grande.
Parece ser un problema de carácter elemental, y a simple vista no es claro el porque genera tanto interés. Una razón, para mi importante, es que está muy relacionado con los grupos de homotopía de los CW complejos (hay que notar que si se considera el esqueleto de un CW-complejo cocientado por el
-esqueleto no queda otra cosa que una suma de esferas
-dimensionales, por lo tanto, calcular la homotopía de las esferas es un paso necesario para conocer los grupos de homotopía de los CW-complejos (por definiciones de estos conceptos, ver este post, de todas maneras, el post actual es elemental, y no es necesario haber comprendido este párrafo).
Nos interesaremos en este post por conocer los más fáciles de calcular, los que de hecho parecen evidentes, con
.
La primera observación es que son, como se puede esperar, todos triviales. Es decir, todo mapa continuo con
es homotópico a un punto. De hecho, supongamos que
no es sobreyectiva (cosa razonable dado que
), obtenemos entonces que como
menos un punto es
se cumple que
es homotópico a la función constante.
El problema es que no podemos asumir a priori que no es sobreyectiva (de hecho podría serlo y no es difícil construir un ejemplo usando la curva de Peano o sus variantes) y resulta no tan inmediato ver que podemos hacer a
homotópica a una función no sobreyectiva.
En realidad, lo que vamos a probar prueba (con iguales argumentos) el siguiente teorema conocido como «de aproximación celular».
Teorema (de Aproximación Celular) Sea
un mapa entre CW-complejos. Entonces,
es homotópico a un mapa celular (es decir, tal que el mapa restricto al
esqueleto
de
se mapea en el
esqueleto
de
).
La idea es contar 2 enfoques, el primero, tiene que ver con topología diferencial y el segundo es más bien topológico. Voy a concentrarme en el segundo y espero que quede claro porque.
Enfoque diferencial.
La idea es que todo mapa continuo entre variedades diferenciables es aproximable por un mapa diferenciable (por una prueba ver aquí).
El bien conocido Teorema de Sard dice (en particular) que si es un mapa diferenciable entre variedades y
entonces se verifica que
no puede ser sobreyectiva. Aprovecho para preguntar si alguien conoce una prueba (más simple que la del teorema de Sard, obvio) de esta «particularización» del Teorema de Sard?.
Como dos mapas suficientemente cerca son homotópicos, probamos de esta manera que todo mapa continuo con
es homotópico a un mapa no sobreyectivo y por tanto, a un punto como dijimos antes.
La razón por la cual no soy fanático de este enfoque es que no conozco una prueba «simple» de que un mapa diferenciable no es sobreyectivo. Por eso, voy a continuar con el enfoque topológico que tiene sus partes lindas.
Enfoque topológico.
No se si vale la pena aclaralo, pero nos basamos en el libro de Hatcher.
Lo primero que voy a hacer es contar la prueba para el caso del grupo fundamental, es decir, la prueba de que las esferas de dimensión son simplemente conexas. Digamos que la idea de la prueba está ahi, pero el hecho de que el círculo es de dimensión uno simplifica un poco el asunto.
Proposición Para todo
se tiene que
.
Demostración: Consideramos una función continua. Queremos ver que es homotópica a una función no sobreyectiva.
Para eso, consideramos un hemisferio abierto de
y nos fijamos en
que es un abierto en
. Podemos suponer que
no es todo
sino ya se verifica que
no es sobreyectiva.
Obtenemos que es una unión (a lo sumo) numerable de intervalos abiertos. Además, la imágen de los bordes de dichos intervalos se encuentra en
. Fijado
, por compacidad de
, obtenemos que solo finitos de esos intervalos tienen preimagenes de
. Mediante una homotopía fácil de realizar de esas finitas curvas al borde de
, hacemos una homotopía que transforma a
en un mapa no sobreyectivo.
Evidentemente esta prueba hace uso que en el caso de dimensión uno, sabemos siempre que todo abierto es unión de intervalos lo cual hace un tanto más simple el asunto.
El remate de la prueba podría haber sido cambiado de forma de mandar todo lo que entra a al borde de
mediante una cadena de numerables homotopías (simplemente para comentar una alternativa a la prueba).
Ahora, vamos a pasar a ver como hacer en el caso general. La idea es similar, simplemente hay que identificar que partes pasan «por un punto» y homotopar dichas partes para que dejen de pasar por ahi.
Proposición. Sea
un mapa continuo con
. Entonces,
es homotópico a un mapa que no es sobreyectivo.
Demostración. Consideramos en dos bolas compactas, centradas en un punto
una adentro de la otra
.
Ahora, estudiamos que pasa con . Observamos que el primer y último conjunto son compactos en
mientras que el del medio es abierto (notar que no necesariamente se cumple que
).
Llamamos a un número menor que la distancia entre
y
y que la mitad del radio de
. Por continuidad uniforme, existe
tal que dos puntos en
a distancia menor a
se mapean en puntos a distancia menor que
. Podemos suponer que
es menor que la distancia entre
y
(son dos compactos).
Ahora, cuadriculamos de forma tal que cada prisma de la cuadriculación tenga diametro menor que
. Consideramos entonces
como la unión de los prismas que intersectan
y como
los prismas que intersectan
(es decir una especie de corona de
). Obtenemos que
.
Ahora, vamos a pasar a triangular cada prisma de la cuadriculación. La razón por la cual cuadriculamos primero en vez de triangular de una es para obtener que sea un entorno de
. La razón por la cual luego triangulamos es que los simplices se portan mejor que los prismas con los mapas lineales (determinar la imagen de los vertices de un simplice determinan un único mapa lineal entre simplices, mientras que un prisma tiene condiciones extra para poder extenderse a un mapa lineal).
La idea ahora es: A los triangulos de los vamos a homotopar a mapas lineales en triangulos y vamos a corregir esto en el espacio entre
y
. Esto va a permitir probar que hay una parte a la cual se accede únicamente por estos mapas «lineales» y en ese lugar, obviamente el mapa no será sobreyectivo.
Consideramos continua que verifica que
en
y vale
fuera de
. Llamamos
a los simplices de
.
Ahora, consideramos mapas en el símplice
cada simplice de
el mapa que manda afínmente el simplice coincidiendo con
en los vértices de dicho simplice. Consideramos entonces la homotopía en cada uno de esos simplices vale exactamente
. Notar que como los
coinciden en los bordes correspondientes, esto es una homotopía continua que se extiende a todo
continuamente (y que no hace nada fuera de
). Obtenemos que
es una homotopía entre
y
.
Tenemos que ver que el mapa no es sobreyectivo. Consideramos a
la bola también centrada en
de la mitad de radio. La primera observación es que
manda los puntos de fuera de
fuera de
(esto es directo pues fuera de
la homotopía es constante y para
se verificaba).
Por otra parte, consideramos un simplice en
y por como elegimos
, obtenemos que
está contenido en una bola de radio
alrededor de un punto fuera de
. Por lo tanto,
no intersecta
. Como la homotopía manda cada punto de
a traves de una geodésica, hacia la envolvente convexa de los vertices, obtenemos que
tampoco intersecta
.
Para finalizar la prueba, alcanza ver que la imágen por de
corta
en finitos hiperplanos de dimensión
que evidentemente no pueden rellenarla. Por lo tanto,
no es sobreyectiva y concluimos la prueba (notar que este paso, si bien parece evidente, utiliza el Teorema de Invariancia del Dominio, habrá un argumento más simple?).
[…] Coloquio Oleis los seguidores de Manolo « Grupos de homotopía (no tan) superiores de las esferas. […]
[…] In Análisis Real y Complejo on Viernes 5, Noviembre, 2010 at 3:08 pm En algunos post pasados (este y este) estudiamos formas de probar que un mapa de en con siempre podia ser perturbado a un mapa […]
por qué es necesario que la aplicación f sea no sobreyectiva??
No es que sea necesario que la aplicación no sea sobreyectiva, sólo que cuando no es sobreyectiva sabemos hacer una homotopía a una constante que es lo que buscamos. Es por eso que el primer paso es encontrar una homotopía que haga que la aplicación deje de ser sobreyectiva en caso que lo fuera.
en la demostracion de pi_1(S^n)=0, ¿podrías explicar el final, a partir de que la antiimagen de x está en un número finito de intervalos(incluido eso)? Es que no lo veo…
Gracias
Como es continua, la preimágen de
es continua, la preimágen de  es un conjunto cerrado del círculo
es un conjunto cerrado del círculo 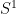 , y por lo tanto compacto (pues el círculo es compacto). La preimagen de
, y por lo tanto compacto (pues el círculo es compacto). La preimagen de  también es un abierto del circulo pues
también es un abierto del circulo pues  es continua, y por como es la topologia del circulo es una union (a lo sumo) numerable de intervalos. Un cubrimiento por abiertos de un compacto tiene un subcubrimiento finito y por tanto hay finitos de esos intervalos que intersectan la preimagen de
es continua, y por como es la topologia del circulo es una union (a lo sumo) numerable de intervalos. Un cubrimiento por abiertos de un compacto tiene un subcubrimiento finito y por tanto hay finitos de esos intervalos que intersectan la preimagen de  . Cada uno de esos intervalos se mapea por
. Cada uno de esos intervalos se mapea por  en una curva contenida en
en una curva contenida en  cuyos extremos estan en
cuyos extremos estan en  y por lo tanto se puede hacer una homotopia para que la curva se haga disjunta de
y por lo tanto se puede hacer una homotopia para que la curva se haga disjunta de  . Después de estas finitas homotopias, tenemos que la imagen de
. Después de estas finitas homotopias, tenemos que la imagen de  es disjunta de
es disjunta de  como queríamos.
como queríamos.