No podés hacer guita en el casino (bajo ciertas hipotesis…)

por Pablo Lessa

Es obvio que se puede hacer guita en el casino. La mejor forma de hacerla es siendo dueño del mismo. La segunda mejor es jugar a un juego de azar en las que uno tiene las de ganar (por ejemplo si tenés buena memoria y concentración el blackjack puede ser un juego así) claro que en ese caso lo más probable es que te rajen.

También podés hacer guita si vas y jugás a un juego de azar en el que tenés las de perder, ponele jugas a la ruleta (supongamos que la ruleta está bien construida de manera de evitar la gran Jagger).

Lo que voy a intentar argumentar entonces es que, si jugás juegos de azar en las que tenés la de perder, utilizando alguna estrategia del estilo «si llego a tanta plata paro».  Entonces en promedio vas a salir con menos plata de la que empezaste.

Homeomorfismos que preservan area en el anillo.

por Rafael Potrie

La idea es comentar un poco sobre el estudio de homeomorfismos del anillo empezado por Poincare y Birkhoff.

Para empezar, contar un poco de lo poco que se de las motivaciones de este estudio. En particular, del punto de vista que viene de la mecanica clasica. Intentare dar algunas ideas medio heuristicas intentando evitar definiciones pesadas.

Los sistemas hamiltonianos son sistemas de ecuaciones diferenciales cuyas soluciones preservan algun tipo de energia, por su calidad de sistemas mecanicos, donde no solo importa la posicion sino tambien la velocidad, estamos frente a sistemas de dimension par. Estos sistemas van a ser consevativos, preservan esa energia que comentamos, por lo tanto, los espacios de energia constante van a ser invariantes y tener dimension una dimension menor.

Si tomamos una orbita regular del flujo hamiltoniano (es decir, donde el campo no se anula), podemos trazar una subvariedad transversal al flujo donde podremos definir un mapa de primer retorno (supongamos por ejemplo que el punto es recurrente, o una orbita periodica). Lo interesante, es que ese mapa de primer retorno tambien preservara una forma de volumen en esa subvariedad de codimension 2 en la variedad inicial (de hecho, tb preserva una forma simplectica ahi, algo mucho mas restrictivo aun).

Supongamos entonces que estamos frente a un sistema de ecuaciones diferenciales hamiltonianas en de dimension 4 (en esto se intereso Poincare, intentando estudiar cualitativamente el problema de 3 cuerpos en el plano y haciendo algunas simplificaciones), entonces, vamos a asumir que tenemos una orbita periodica, y que si nos fijamos en el retorno que definimos en el parrafo anterior, su derivada tiene valores propios complejos conjugados que no son raiz de la unidad.

En dicho caso, no podemos utilizar el conocido teorema de Hartman y Grobman que nos permite conjugar la dinamica cerca del punto fijo a su parte lineal. Pero siendo que 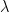no es raiz de la unidad hay un simil de dicho teorema que nos da anillos invariantes (teoria KAM) lo cual motiva sin duda el estudio de homeomorfismos como en el titulo de esta nota.

Entropia y topología.

por Rafael Potrie

La idea es dar la prueba de un teorema de Manning que relaciona la entropía de un homeomorfismo en una variedad con la acción de este en la homología de la variedad, o en el grupo fundamental. Obviamente, antes es necesario definir estos conceptos, y en la medida de lo posible motivar la «importancia» del resultado.

ENTROPIA

Voy a empezar por introducir el concepto de entropía de un homeomorfismo. No pretendo ser exhaustivo, sino simplemente introducir una de las posibles definiciones (que es la que voy a utilizar) y en lo posible motivarla un poco.

La idea es dar una «medida» de cuan compleja es la dinámica de un homeomorfismo. En general, fijado un , si queremos conocer la dinamica de los primeros iterados de todos los puntos (modulo , es decir, admitiendo un error de ese valor), nos basta con conocer los primeros iterados de un cierto conjunto finito de puntos (esto es una consecuencia directa de la continuidad uniforme de los primeros iterados del homeomorfismo). La entropia medira entonces, el crecimiento exponencial de dichos conjuntos, lo cual parece una medida razonable de la complejidad.