Topologias en conjuntos finitos

por Andrés Sambarino

Voy a parafrasear este artículo de wikipedia que me dejó como loco.

El asunto es poner una topología en un conjunto de 4 elementos, y ver que el grupo fundamental es La cosa es así: Considerás con la topología

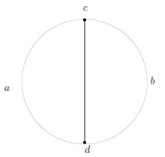Se puede construir fácil una función contínua sobreyectiva del círculo en como en el dibujo: Consideramos el círculo como vectores de norma 1 en y definimos

y

Para calcular el grupo fundamental, la idea es ver que el espacio es union de dos abiertos contractibles, y cuya intersección son dos conjuntos contractibles. Para ver que es contractible basta observar que es abierto y es cerrado y considerar el mapa dado por

para y para

En esta situación no se puede usar el teorema de van Kampen, porque la intersección de con no es conexa, pero parece que hay una generalizacion que permite usar van Kampen con varios puntos base.

Resulta ademas, que en este artículo, McCord prueba que cualquier CW complejo finito (finitas celulas) es debilmente homotopicamente equivalente (i.e. hay una función que es un isomorfismo en todos los gruos de homotopia) a una topología en un conjunto finito…

 

 

 

 

 

Conjuntos ambiente homogeneos

por Rafael Potrie

El objetivo de este post es presentar un resultado que por mucho tiempo me resultó bastante misterioso pero que es sencillo y bastante lindo. Es una caracterización de las subvariedades encajadas a través de propiedades locales de sus encajes.

Para mantener la discusión simple (sin perder generalidad) trabajaremos en . Es fácil ver, dado que todos los argumentos y definiciones son locales, que esto se extiende de forma directa a variedades diferenciables en general.

Sea un conjunto localmente compacto. Decimos que es –ambiente homogeneo si se cumple que para todo par de puntos existen entornos y en de ellos y un difeomorfismo de clase  que manda en y cumple que .

Probaremos un resultado debido a Repovs. Skopenkov y Scepin que afirma que un conjunto -ambiente homogeneo es una subvariedad encajada en . Notar que es un ejercicio sencillo mostrar que las sub-variedades encajadas de clase son efectivamente -ambiente homogeneas. No veremos muchas aplicaciones, referimos al  lector por ejemplo a este paper de Amie Wilkinson que utiliza este resultado y da una prueba del caso . Si mencionamos que este resultado tiene como consecuencia directa que los subgrupos cerrados de un grupo de Lie son grupos de Lie.

Es un ejercicio interesante mostrar que el conjunto de Cantor puede ser encajado en de forma tal de ser Lipschitz ambiente homogéneo. Otro interesante ejercicio es mostrar el resultado para el caso de subconjuntos -ambiente homogeneos de .

Clasificacion de las 1-variedades

por Pablo Lessa

En esta pequeña nota quiero dar una prueba de la clasificación de las variedades diferenciables de dimensión 1.

La otra demostración que conozco (e.g. en el libro de Milnor) utiliza que la variedad puede partirse en piezas que son segmentos parametrizados por longitud de arco, y luego analiza combinatoriamente como se pegan estas piezas llegando a los dos casos:  O se cierran y la variedad es un círculo, o no y la variedad es un intervalo.  Una demostración similar puede llevarse a cabo para variedades topológicas de dimensión 1 y además la demostración captura la escencia de porqué es verdad el resultado.  Cabe preguntarse entonces: ¿Porqué molestarse en dar otra demostración?

Creo que el mérito de la siguiente demostración es que, a pesar de no ser elemental, sólamente utiliza herramientas que son utiles para muchas otras cosas.  Sin más preambulos acá va la demostración.

Teorema: Toda variedad diferenciable conexa de dimensión 1 es difeomorfa a un intervalo o a .

Algunas variedades que no admiten difeomorfismos de Anosov.

por Rafael Potrie

En un post anterior, estudiamos unos trabajos de Franks y Manning acerca de la clasificación de difeomorfismos de Anosov en el Toro . En particular, vimos que para que dicha variedad admita un Anosov, había ciertas restricciones en la clase de homotopía de dicho difeomorfismo (tenía que ser homotópico a un difeomorfismo de Anosov lineal), esto era consecuencia del Teorema de Indice de Lefschetz.

En este post, voy a mostrar como esa idea puede ser levemente empujada en función de obtener más restricciones en la topología de una variedad que admite un difeomorfismo de Anosov (y en particular, en como tiene que actuar en la homología de la variedad).

Una consecuencia particular del estudio, nos va a dar que:

Teorema 1 La esfera no admite difeomorfismos de Anosov.

Notar que al día de hoy, los unicos difeomorfismos de Anosov conocidos son los que aparecen en infranilvariedades (estos estan clasificados hasta dimensión 8, ver aqui), y se sabe también que en dimensión menor o igual a 3, todos tienen que ser difeomorfismos de Toros y estos son los únicos ejemplos en dichas dimensiones. Se conjetura que todos los difeomorfismos de Anosov deberían ser en infranilvariedades (lo cual implicaría que son conjugados a ejemplos algebraicos) y en particular, deberían ser transivos (pero incluso esto último, es un problema abierto).  El Teorema 1  fue probado en este artículo (creo yo que por primera vez, pero no se).

Superficies Esenciales.

por Andrés Sambarino

Supongamos que estamos en la siguiente situación: Tenemos una variedad Riemanniana de curvatura cuyo grupo fundamental es el de alguna superficie hiperbólica El contexto es tal que tenemos

A uno le gustaría decir entonces que contiene una copia de cuyo se inyecta en el de Resulta que esto es cierto y es (relativamente) fácil de demostrar.

Sea el cubrimiento universal de Recordamos que actúa en por isometrías y que

Teorema A. Identificamos con un subgrupo discreto de isometrías de Entonces existe continua y -equivariante, es decir que para todos y se tiene

 

Difeomorfismos de Anosov en el Toro.

por Rafael Potrie

En este post pienso comentar la demostración (debida a Franks y Manning) de que un difeomorfismo de Anosov de una infranilvariedad (un cociente de una nilvariedad) es de hecho conjugado a un difeomorfismo de Anosov lineal. Por simplicidad, me voy a concentrar en el caso de difeomorfismos de Anosov en toros. Vale la pena observar que todos los ejemplos conocidos de difeomorfismos de Anosov lineales son en infranilvariedades (que incluyen obviamente a los toros).

Intentaré siempre poner links a las definiciones necesarias y resultados utilizados ya que no voy a centrarme en rellenar los prerequisitos, pero no creo que alguien que no este familiarizado con los conceptos que aparezcan pueda seguir la prueba.

Grupos fundamentales de variedades y grupos finitamente presentados.

por Rafael Potrie

Me gustaría en este post discutir un poco la relación entre grupos y variedades para mostrar un poco como a veces cosas que parecen ejemplos de una estructura abstracta, en realidad la contienen. Un buen ejemplo, son los grupos de simetrías de espacios finitos, que de hecho contienen absolutamente todos los posibles grupos finitos (y de esa manera, nos permite comprender los grupos desde un punto de vista más geométrico).

En este post, voy a ver la relación entre los grupos finitamente presentados y los grupos fundamentales de variedades. Vamos a mostrar que un grupo es finitamente presentado si y solamente si es el grupo fundamental de una variedad. De hecho, mostraremos esto para variedades (pero es válido para variedades de cualquier dimensión mayor o igual a ).

Antes de empezar, mismo antes de definir grupo finitamente presentado, voy a dar un argumento (rápido) de porque en dimensiones dos y tres esto no es posible. Lo único a decir sobre los grupos finitamente presentados, es que naturalmente, los grupos finitos lo son.

En dimensión dos, tenemos bien definida una lista de variedades, con lo cual es fácil ver que grupos como no son grupo fundamental de ninguna superficie.

En dimensión tres, argumentos parecidos pueden ser hechos, uno rápido es tener en cuenta que toda -variedad con grupo fundamental finito tiene que ser cubierta por la -esfera (esto lo sabemos gracias a que recientemente la conjetura de Poincare en dimensión fue demostrada) y se sabe que no todo grupo finito puede actuar libre y discontinuamente en la -esfera (esto hay que chequearlo, pero a mi al menos me resulta suficientemente convincente).

Grupo fundamental de las esferas.

por Rafael Potrie

En el post anterior, se discutió una prueba de que el grupo fundamental de las esferas de dimensión () es trivial. Escencialmente, la prueba consistía en hacer una homotopía de un mapa a un mapa que no fuese sobreyectivo (eso permite concluir ya que la esfera menos un punto es contractible, como se puede ver utilizando la proyección estereográfica).

En este post, pretendo dar una prueba «distinta» de este hecho. Las comillas tienen que ver con que es realmente difícil definir que es que dos pruebas sean la misma o no (por una discusión sobre esto, recomiendo este post). Luego de dar la prueba, voy a comentar porque me parece (al menos un poco) distinta.

Grupos de homotopía (no tan) superiores de las esferas.

por Rafael Potrie

Uno de los problemas más difíciles de la topología algebraica es determinar los con grande.

Parece ser un problema de carácter elemental, y a simple vista no es claro el porque genera tanto interés. Una razón, para mi importante, es que está muy relacionado con los grupos de homotopía de los CW complejos (hay que notar que si se considera el esqueleto de un CW-complejo cocientado por el -esqueleto no queda otra cosa que una suma de esferas -dimensionales, por lo tanto, calcular la homotopía de las esferas es un paso necesario para conocer los grupos de homotopía de los CW-complejos (por definiciones de estos conceptos, ver este post, de todas maneras, el post actual es elemental, y no es necesario haber comprendido este párrafo).

Nos interesaremos en este post por conocer los más fáciles de calcular, los que de hecho parecen evidentes, con .

Reparametrizaciones de flujos de Anosov

por Andrés Sambarino

Si tenemos un flujo y una función estrictamente positiva y contínua podemos reparametrizar el flujo usando de la siguiente manera: Sea dada por