Lema de los Lideres y Teorema Ergódico en el caso ergódico

In Uncategorized on domingo 7, junio, 2009 at 5:37 pm

Consideremos la siguiente sucesión finita de números reales:

$10,-15,2,-1,5,-6,22,-3$

Decimos que un término es «lider» si alguna de las sumas de elementos consecutivos a partir de él es menor o igual a cero.

Los términos $-15,-1,-6,-3$ son trivialmente lideres, pero también $10$ porque $10 - 15 \le 0$ , $2$ porque $2 -1+5-6 \le 0$ , y por último $5$ porque $5 - 6 \le 0$ .

O sea que la lista de lideres es:

$\{10,-15,2,-1,5,-6,-3\}$

La observación es que la suma de estos números es menor o igual a cero.

Formalizamos la definición como sigue:

Definición (lider).

Si $x_1,\ldots,x_n \in \mathbb{R}$ decimos que un término $x_k$ es lider en la sucesión si existe $l\in\{k,k+1,\ldots,n\}$ tal que:

$x_k + x_{k+1} + \cdots + x_l \le 0$

El lema del lider entonces es el siguiente (observamos que se está utilizando la convención de que una suma vacía vale cero):

Lema de los lideres (F. Riesz).

Si $x_1,\ldots,x_n \in \mathbb{R}$ y

$L = \{k \in \{1,\ldots,n\}: x_k\text{ es lider en }x_1,\ldots, x_n\}$

entonces

$\sum_{k \in L}x_k \le 0$

El siguiente lema trata de sucesiones estacionarias de variables aleatorias, cosa definida en este artículo. Hablando mal y pronto se puede pensar $X_n = f\circ T^n$ donde $T: X \to X$ preserva una medida de probabilidad y $f: X \to \mathbb{R}$ es medible (y se tiene el hábito funky de utilizar $P, E$ para denotar la medida y la integral respectivamente y $1_A$ para denotar la función característica de un conjunto $A$ , entre otras convenciones notacionales).

Lema (Karlsson-Margulis).

Sea $X_1,\ldots, X_n,\ldots$ una sucesión estacionaria de variables aleatorias tal que $E(X_n) > 0$ para todo $n$ .

Para cada $n$ definamos $S_n = X_1 + \cdots + X_n$ .

Se cumple que:

$P(S_n > 0\text{ para todo }n) > 0$ .

Demostración. Para cada $n$ aplicamos el lema de los lideres a la sucesión $X_1,\ldots, X_n$ obteniendo:

$\sum_{k \le n}X_k1_{\{X_k\text{ lider en }X_1,\ldots,X_n\}} \le 0$

Dado que la condición de ser lider solo depende de los siguientes términos se tiene:

$\sum_{k \le n}X_k1_{\{X_k\text{ lider en }X_k,\ldots,X_n\}} \le 0$

Tomando esperanza

$\sum_{k \le n}E(X_k1_{\{X_k\text{ lider en }X_k,\ldots,X_n\}}) \le 0$

utilizando la estacionariedad

$\sum_{k \le n}E(X_11_{\{X_1\text{ lider en }X_1,\ldots,X_{n+1-k}\}}) \le 0$

cambiando de nombre los índices y utilizando la definición:

$\sum_{k \le n}E(X_11_{A_k}) \le 0\text{ donde }A_k = \{S_j \le 0\text{ para algun }j\le k\}$ .

Observemos que $A_k \subset A_{k+1}$ .

Si se tuviera $P(A_k) \to 1$ cuando $k \to +\infty$ entonces dado que $E(X_1) > 0$ se tendría a partir de cierto $k$ que los sumandos $E(X_11_{A_k})$ serían positivos y mayores a $E(X_1)/2$ . Esto contradice la validez para todo $n$ de la desigualdad obtenida anteriormente $\Box$

Con esto obtenemos el teorema ergódico en el caso ergódico casi sin problemas:

Teorema Ergódico de Birkhoff: Caso Ergódico

Supongamos que $X_1,\ldots, X_n,\ldots$ es una sucesión estacionaria de variables aleatorias tal que $E(X_n) = A$ para todo $n$ . Y tomemos $S_n$ como en el lema anterior.

Si se tiene que:

$\text{liminf}(\frac{S_n}{n})$

y

$\text{limsup}(\frac{S_n}{n})$

son constantes en un conjunto de probabilidad $1$ entonces, son iguales a $A$ con probabilidad $1$ .

Demostración. Sea $a < A$ . Del lema anterior se deduce (tomando la sucesión $\{X_n - a\}$ ) que:

$P(\frac{S_n}{n} > a\text{ para todo } n) > 0$

y por lo tanto

$P(\text{liminf}(\frac{S_n}{n}) \ge a) > 0$

de lo cual se tiene por la ergodicidad:

$P(\text{liminf}(\frac{S_n}{n}) \ge a) = 1$

Esto implica que $\text{liminf}(\frac{S_n}{n}) \ge A$ en un conjunto de probabilidad $1$ .

Razonando con $2A-X_n$ se obtiene $2A - \text{limsup}(\frac{S_n}{n}) \ge A$ o lo que es lo mismo $\text{limsup}(\frac{S_n}{n}) \le A$ en un conjunto de probabilidad $1$ . De esto se obtiene el resultado $\Box$

Preguntas

¿Alguién tiene una prueba corta y elegante del lema de los lideres? ¿Se puede arreglar la demostración del teorema ergódico para que funque en el caso no ergódico (ya sea por un argúmento utilizando Krein-Milman para aproximar medidas no ergódicas por combinaciones de ergódicas, o por algúna modificación del argumento)? ¿Está bien la prueba esta (el lema lo extraje como caso particular de un laburo de Karlsson-Margulis del 99, ellos prueban un teorema ergódico (de Kingman) más fuerte con su lema así que trate de inventar una prueba del de Birkhoff como ejercicio)?

▶ 5 respuestas

¿Que les parece la siguiente prueba del teorema ergódico en el caso general?

Si $\text{limsup} - \text{liminf}$ integra positivo para algúna medida invariante, entonces utilizando Krein-Milman se obtiene que integra positivo para alguna medida invariante y ergódica. Absurdo si conocemos el teorema en el caso ergódico.

¡Yo sabía que el pique de safar del teorema de descomposición ergódica utilizando Krein-Milman, que me enseño el Gordo, me iba a servir!

Responder

pablolessa 7 junio 2009 at 5pm
Ta muy buena la prueba! Voy a tener que leerla de nuevo por el tema probabilistico que me cuesta… mejor cpaz te pido que me la cuentes.

Tengo una cosa que no se si es prueba (y menos si es corta y/o elegante) del lema de los lideres, pero capaz sirve como idea.

Me parece que si te fijas en la suma que define a un elemento como lider. En caso que sea positivo el numero, tiene que haber otro lider en ella. Por lo tanto, la suma de los lideres ahi es menor o igual a cero. Creo que eso implica que la suma de todos los lideres tiene que ser menor o igual a cero.

Dicho de otra manera, como los elementos que no son lideres son necesariamente positivos, si la suma de los lideres es positiva, alguno de ellos necesariamente no va a ser lider lo cual es absurdo (si los tenes ordenados, el primero tal que todas las sumas para adelante son positivas no puede ser lider).

No se, creo que es una prueba y no esta mal… pero puede que haya pifiado con la definicion de lider.

Responder

Rafael Potrie 7 junio 2009 at 6pm
Me parece que está perfect tu prueba gordo. La trato de escribir…

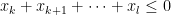Parte 1: Si $x_k$ es lider y $x_k + x_{k+1} + \cdots + x_l \le 0$ entonces se cumple $\sum_{i \in L, k \le i \le l} x_i \le x_k + \cdots + x_l \le 0$ (suma de los lideres entre $k$ y $l$ es menor o igual al cero). Esto es cierto porque los no-lideres son positivos.

Parte 2: Si no hay lideres en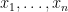 $x_1,\ldots,x_n$ entonces es cierto el enunciado. Si $x_k$ es el primer lider sabemos que la suma de los lideres contenidos en cierto intervalo no vacio $\{1,\ldots,k,\ldots, l\}$ es menor o igual a cero. Borramos ese intervalo y usamos inducción (ya que la propiedad de que un término sea lider depende solo de los términos posteriores a él).

Responder

pablolessa 7 junio 2009 at 6pm
Hoy mirando el arxiv encontré:
«Heaviness: An Extension of a Lemma of Y. Peres» de «David Ralston»
http://arxiv.org/abs/0906.4001

El lema de Peres es simplemente el lema de Karlsson-Margulis en el contexto donde hay topología.

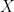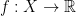Básicamente la cosa es así: Sea $X$ espacio topológico compacto y $T:X \to X$ continua que preserva cierta probabilidad boreliana $\mu$ . Entonces para toda $f:X \to \mathbb{R}$ continua los conjuntos:

$\{x \in X: \frac{1}{n}\sum_{k = 0}^{n-1}f(T^kx) \ge a\text{ para todo }n\}$

son compactos, y por Karlsson-Margulis miden positivos para todo $a < \int f\mathrm{d}\mu$ . Por lo tanto su intersección es no vacia y existe un punto con:

$\frac{1}{n}\sum_{k = 0}^{n-1}f(T^kx) \ge \int f \mathrm{d}\mu$

para todo $n$ .

Responder

pablolessa 23 junio 2009 at 2pm
[…] o el Teorema Ergódico de Birkhoff (una prueba de este último bastante simple se encuentra en este link de este mismo […]

Responder

Medidas invariantes y Teorema de Descomposición Ergódica. « Coloquio Oleis 29 abril 2010 at 10am