Crecimiento asintótico de órbitas periódicas.

dinamica hiperbolica, Funcion zeta, shift, sub-shift de tipo finito, subshift

Crecimiento asintótico de órbitas periódicas.

In Sistemas Dinámicos on miércoles 17, marzo, 2010 at 5:26 pm

Sea $f:X\to X$ un sistema dinámico con un numero finito de órbitas periódicas de cada período. Consideramos

$\nu_n=\#\{x\in X: f^n(x)=x\}$

el número de puntos fijos de $f^n$ y la siguiente serie de potencias llamada función zeta: $\zeta:\mathbb C\to\mathbb C$ dada por

$\zeta(z)=\exp \sum_{n=1}^\infty \frac{z^n}n \nu_n.$

Parecería que esta función contiene información dinámica, aunque no queda claro como convertir información sobre la función $\zeta$ (por ejemplo, su radio de convergencia) en información sobre el sistema dinámico $f.$ Nuestro objetivo es entonces mostrar cómo utilizando esta función se puede demostrar un teorema de crecimiento de órbitas periódicas para sub-shifts de tipo finito. Más precisamente, sea

$\pi(x)=\#\{\textrm{\'orbitas peri\'odicas de per\'iodo}\leq x\}=\sum_{\lambda(\tau)\leq x} 1$

donde $\lambda(\tau)$ es el período de la órbita periódica $\tau.$ El objetivo es demostrar el siguiente teorema:

Teorema[Parry] Sea $\sigma:\Sigma_A\to\Sigma_A$ un sub-shift de tipo finito irreducible. Entonces existe $\beta>1$ tal que

$x\beta^{-x}\pi(x)\to \beta/(\beta-1)$

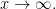
cuando $x\to\infty.$ $\beta^{-1}$ es el radio de convergencia de la serie $\sum_{n=1}^\infty \frac{z^n}n \nu_n.$

Como observación comentamos que además $\log \beta$ es la entropía topológica de $\sigma,$ pero ese ya es otro teorema. El artículo esta basado en el libro de Parry-Pollicott «Zeta Functions and the periodic orbit structure of hiperbolic dynamics».

Sub-shifts de tipo finito.

Comenzamos por explicar qué es un sub-shift de tipo finito.

Dado un conjunto finito de símbolos (o alfabeto) $\{1,\cdots, k\}$ consideramos el espacio $\Sigma={\{1,\cdots,k\} }^{\mathbb Z}$ de todas las sucesiones bilaterales de elementos de $\{1,\cdots,k\}.$ Este espacio es metrizable y topológicamente es un conjunto de Cantor. Tenemos una transformación natural llamada shift, $\sigma :\Sigma\to\Sigma$ dada por $\sigma(\{x_n\})=\{x_{n+1}\}.$

Sea $A$ una matriz $k\times k$ cuyas entradas $A(i,j)$ consisten en ceros o unos. Esta matriz induce un subconjunto $\sigma$ -invariante, que llamamos $\Sigma_A,$ de la siguiente forma:

$\{x_n\}\in \Sigma_A \Leftrightarrow$ para todo $n\in\mathbb Z$ vale que $A(x_n,x_{n+1})=1.$

Es decir, si $A(i,j)=0$ entonces ninguna sucesión de $\Sigma_A$ tiene $ij$ como una subpalabra. El sistema dinámico $\sigma:\Sigma_A\to\Sigma_A$ es lo que se llama un sub-shift de tipo finito.

Si existe $n>0$ tal que todas las entradas de $A^n$ son positivas decimos que $A$ es irreducible. En este caso el sistema dinámico $\sigma:\Sigma_A\to\Sigma_A$ es transitivo y sus órbitas periódicas son densas.

La Función zeta.

Estudiamos entonces propiedades de la función zeta para un sub-shift de tipo finito irreducible $\sigma:\Sigma_A\to\Sigma_A$ que quedará fijo de aquí en mas. Como una potencia de $A$ tiene todas sus entradas positivas, aplicamos el teorema de Perron-Frobenius a $A^n:$

Teorema[Perron-Fröbenius]. Sea $M$ una matriz con coeficientes estrictamente positivos, entonces $M$ tiene un único valor propio de módulo máximo y este valor propio es simple, es decir, el espacio propio asociado tiene dimensión 1.

Obtenemos que $A$ tiene un único valor propio de módulo maximo, $\beta.$ Es fácil ver que $\beta$ es real e incluso tenemos que $\beta>1.$ Podemos demostrar entonces la primer proposición:

Proposición. El radio de convergencia de la serie

$\sum_{n=1}^\infty \frac{z^n}n \sum_{\{x\in\Sigma_A:\sigma^n x=x\}}1$

es $\beta^{-1}.$

Demostración. Recordemos que $\nu_n=\sum_{\{x:\sigma^n x=x\}}1.$ El radio de convergencia de la serie se calcula entonces como el $\liminf_n (\nu_n/n)^{-1/n} =\liminf_n \nu_n^{-1/n}.$ Vamos a probar que

$\frac 1n\log \sum_{\{x:\sigma^n x=x\}}1\to \log\beta.$

La observación clave para probar esto es ver que

(0) $\sum_{ \{x:\sigma^n x=x\} }1=\textrm{Traza}(A^n).$

Para esto utilizamos una formula general para calcular la traza de una potencia de una matriz dada:

$\textrm{Traza} (A^n)=\sum_{1\leq i_1,\cdots,i_n\leq k}A(i_1,i_2)\cdots A(i_n,i_1).$

Recordamos que los coeficientes $A$ son $0$ o $1,$ y entonces el producto $A(i_1,i_2)\cdots A(i_n,i_1)=1$ quiere decir exactamente que la palabra $i_1i_2\cdots i_ni_1$ pertenece a $\Sigma_A,$ es decir, un punto fijo de $\sigma^n.$ Queda entonces probada la fórmula (0).

Sean $\beta,\lambda_1,\cdots, \lambda_l$ los valores propios de $A$ (que pueden ser complejos). Sabemos del teorema de Perron-Fröbenius que $|\lambda_i|<\beta$ para todo $i,$ de esto último se deduce que:

$\frac 1n\log \sum_{\{x:\sigma^n x=x\}}1=\frac 1n \log \textrm{Traza}(A^n)=$

$=\frac 1n \log \{\beta^n+\lambda_1^n+\cdots+\lambda_l^n\}\to \log\beta.$

$\square$

Dos fórmulas para la función zeta.

En esta sección vamos a demostrar dos formas de escribir $\zeta$ que reflejan diferentes aspectos.

Proposición 1. $\zeta(z)=\frac 1{\det(I-zA)}$

Demostración. A partir de la ecuación (0) tenemos que

$\zeta(z)=\exp \sum_{n=1}^\infty \frac{z^n}{n}\textrm{Traza}(A^n)=\exp \sum_{n=1}^\infty \frac{z^n}n (\beta^n+\lambda_1^n+\cdots+\lambda_l^n)=$

$=\exp \sum_{n=1}^\infty \frac{(\beta z)^n}{n}+\sum_{k=1}^l \frac{(\lambda_iz)^n}{n}$

Aplicamos entonces el desarrollo de Taylor de $\log(1-x)$ :

$\log(1-x)=-\sum_{n=1}^\infty \frac{x^n}n.$

y obtenemos entonces $=\exp \left \{- \log(1-\beta z)(1-\lambda_1z)\cdots(1-\lambda_lz)\right\} = \frac 1{\det(I-zA)}$

$\square$

A la fórmula de la proposición 1 le llamaremos (1).

Proposición 2. Si $\tau$ denota una órbita periódica de $\sigma$ y $\lambda(\tau)$ su período entonces tenemos que

${\displaystyle\zeta(z)=\prod_{\tau-\textrm{\'orbita peri\'odica}} (1-z^{\lambda(\tau)})^{-1}}$

Esta será llamada ecuación (2).

Demostración. ${\displaystyle \sum_{n=1}^\infty \frac{z^n}n \sum_{\{x:\sigma^n x=x\}}1}=$

${\displaystyle\sum_{n=1}^\infty\sum_{\sigma^n(x)=x,\ n\textrm{-m\'inimo}}\sum_{k=1}^\infty \frac{z^{kn}}{kn}= \sum_{\tau\textrm{-\'orbita peri\'odica}} \sum_{k=1}^\infty \frac{z^{\lambda(\tau)k}}k }$

Aplicando nuevamente el desarrollo del logaritmo tenemos que

$\zeta(z)=\exp \sum_{\tau\textrm{-\'orbita peri\'odica}}-\log(1-z^{\lambda(\tau)})=\prod_{\tau\textrm{-\'orbita peri\'odica}}(1-z^{\lambda(\tau)})^{-1}$

$\square$

Demostración del teorema de Parry.

La expresión (2) para la función zeta nos da una cota superior para el creciemiento de la función $\pi(x)=$ cantidad de órbitas periódicas de período $\leq x.$

Lema 1. Para todo $\gamma>1$ se tiene que $\beta^{-\gamma x}\pi(x)\to 0$ cuando $x\to\infty.$

Demostración. Como $\zeta(z)$ converge para todo $|z|<\beta^{-1}$ tenemos que

$\zeta(\beta^{-\gamma})=\prod_{\tau\textrm{-\'orbita peri\'odica}}(1-\beta^{- \gamma\lambda(\tau)})^{-1}\geq$

$\prod_{\tau}(1+\beta^{-\gamma\lambda(\tau)})$

(simplemente porque $(1+x)\leq 1/(1-x)$ ). El término anterior es mayor o igual que

$\prod_{\tau: \lambda(\tau)\leq x}(1+\beta^{-\gamma x}) \geq$

${\displaystyle (1+\beta^{-\gamma x})^{\pi(x)} \geq 1+\pi(x)\beta^{-\gamma x}}.$

Tenemos entonces que $\pi(x)\beta^{-\gamma x}$ está acotado por una cota que no depende de $\gamma>1,$ concluimos entonces que $\pi(x)\beta^{-\gamma x}\to 0.$

$\square$

Recordamos que si $\beta, \lambda_1,\ldots, \lambda_l$ son los valores propios de $A$ entonces se tiene que $|\lambda_i|<\beta$ lo que implica, usando la ecuación (1), que

$\frac{\zeta'(z)}{\zeta(z)}=\frac {\beta}{1-\beta z}+\alpha(z)$

donde $\alpha$ es holomorfa en un disco de radio $\exp(\varepsilon)\beta^{-1}$ para algún $\varepsilon$ suficientemente pequeño. (Esto se ve con un cálculo explicito de $\zeta'(z)/\zeta(z)$ observando que en el denominador solo quedan terminos de la forma $1-\lambda_i z$ ).

El hecho de que el radio de convergencia de $\alpha$ sea mayor que el de $\zeta$ es un punto clave en la demostración como veremos en los pasos siguientes.

De la ecuación (2) y del cálculo anterior obtenemos (usando nuevamente el desarrollo del logaritmo) que:

$\frac{\zeta'(z)}{\zeta(z)}=\frac 1z\sum_{\tau, n\in\mathbb N}\lambda(\tau)z^{\lambda(\tau)n}=$ $\frac 1z \sum_{n=1}^\infty \beta^nz^n +\alpha(z)$

donde el radio de convergencia de $\alpha(z)$ es $\exp(\varepsilon)/\beta$

Para simplificar la notación consideramos $n\lambda(\tau)$ como el «período» de la órbita $\tau$ recorrida $n$ veces, las órbitas periódicas contadas con multiplicidad las notaremos $\tau'$ y ponemos $\Lambda(\tau')$ al verdadero período, es decir, si $\tau'=\tau^n$ entonces $\lambda(\tau')=n\lambda(\tau)$ y $\Lambda(\tau')=\lambda(\tau)$ . La ecuación de arriba queda entonces

$\frac 1z\sum_{\tau'}\Lambda(\tau')z^{\lambda(\tau')}=$ $\frac 1z \sum_{n=1}^\infty \beta^nz^n +\alpha(z)$

Despejando $\alpha$ tenemos

${\displaystyle \alpha(z)=\sum_{n=1}^\infty z^{n-1}\left(\sum_{\lambda(\tau')=n }\Lambda(\tau')-\beta^n\right)}.$

Como el radio de convergencia de $\alpha$ es $\exp(\varepsilon)\beta^{-1}$ obtenemos para un $\varepsilon$ mas chico que:

$\frac{\exp(\varepsilon n)}{\beta^n}\left(\sum_{\lambda(\tau')=n }\Lambda(\tau')-\beta^n\right)\to0$ cuando $n\to\infty.$

Definimos $\psi(x)=\sum_{\lambda(\tau')\leq x} \Lambda(\tau')$ que, usando el desarrollo para la serie geométrica, es igual a

$\psi(x)=\sum_{n=1}^x \left(\sum_{\lambda(\tau')=n}\Lambda(\tau')-\beta^n\right) +\frac{\beta}{\beta-1}(\beta^x-1)$

Usando la estimación anterior tenemos probado el lema siguiente:

Lema 2. $\left|\psi(x)-\frac\beta{\beta-1}(\beta^x-1)\right|\leq C\frac{\beta^x}{\exp\{\varepsilon x\}}.$

Para terminar solo nos queda relacionar $\pi$ y $\psi:$

$\psi(x)\leq x\pi(x)$
Si $x>y$ entonces $\pi(x)\leq \pi(y)+\psi(x)/y.$

La primer relación, junto con el lema 2 implican que

$\liminf_{x\to\infty} \beta^{-x}x\pi(x)\geq \beta/(\beta-1).$

Si ponemos $x=\gamma y$ con $\gamma>1$ la segunda relación nos da:

$x\beta^{-x}\pi(x)\leq \gamma y \beta^{-\gamma y}\pi(y) +\gamma\beta^{-x}\psi(x)$

Aplicando los lemas 1 y 2 obtenemos

$\limsup_{x\to\infty} x\beta^{-x}\pi(x)\leq \gamma\beta/(\beta-1)$ para todo $\gamma>1.$

Esto concluye la prueba del teorema de Parry.

▶ 2 respuestas

¡Buenísimo el artículo Sambita! ¡Saludos!

Responder

Pablo Lessa 20 marzo 2010 at 1pm
[…] y eso nos hace perder precisión en la estimativa) pero es menos fina que la que se obtiene en este post utilizando la función […]

Responder

Difeomorfismos de Anosov en el Toro. « Coloquio Oleis 5 octubre 2010 at 7am